Eine Regession zur Vorhersage / Erklärung von Häufigkeitsdaten rechnen

Wie berechnet man eine Regression für Häufigkeitsdaten? Eine Poisson-Regression

Möchte man ein Vorhersagemodell auf Häufigkeiten machen, verwendet man eine Poisson-Regression.
Die Idee ist, dass Untergruppen in meinen Daten unterschiedlich häufig ansprechen. Die Nullhypothese lautet, dass die Vorhersage-Gewichte Null sind, die Alternative, dass diese von Null abweichen (d.h. positiv oder negativ mit dem Ansprechen in Form einer Häufigkeit korrelieren) .
Ein Beispiel ist, ob ein Besserungshäufigkeit unter Zieltherapie stärker ausfällt.
Ich würde empfehlen, die Poisson-Regression mit dem R zu rechnen. Kopieren Sie die nachfolgenden Zeilen in Ihr R-Studio.

Die R-Befehlszeilen für ein Mini-Beispiel

mydata = data.frame(gruppe = c(1,1,1,1,2,2,2,2), mycounts = c(1,2,3,3,4,7,9,9)) summary(glm(mycounts ~ factor(gruppe), data = mydata, family="poisson"))

Die R-Ausgabe

Das ergibt den folgenden Ausdruck (wichtig ist nur der fett markierte p-Wert):

Call:
glm(formula = mycounts ~ gruppe, family = "poisson", data = mydata)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.3200 -0.3617 0.1910 0.5131 0.6261
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.8109 0.3333 2.433 0.01498 *
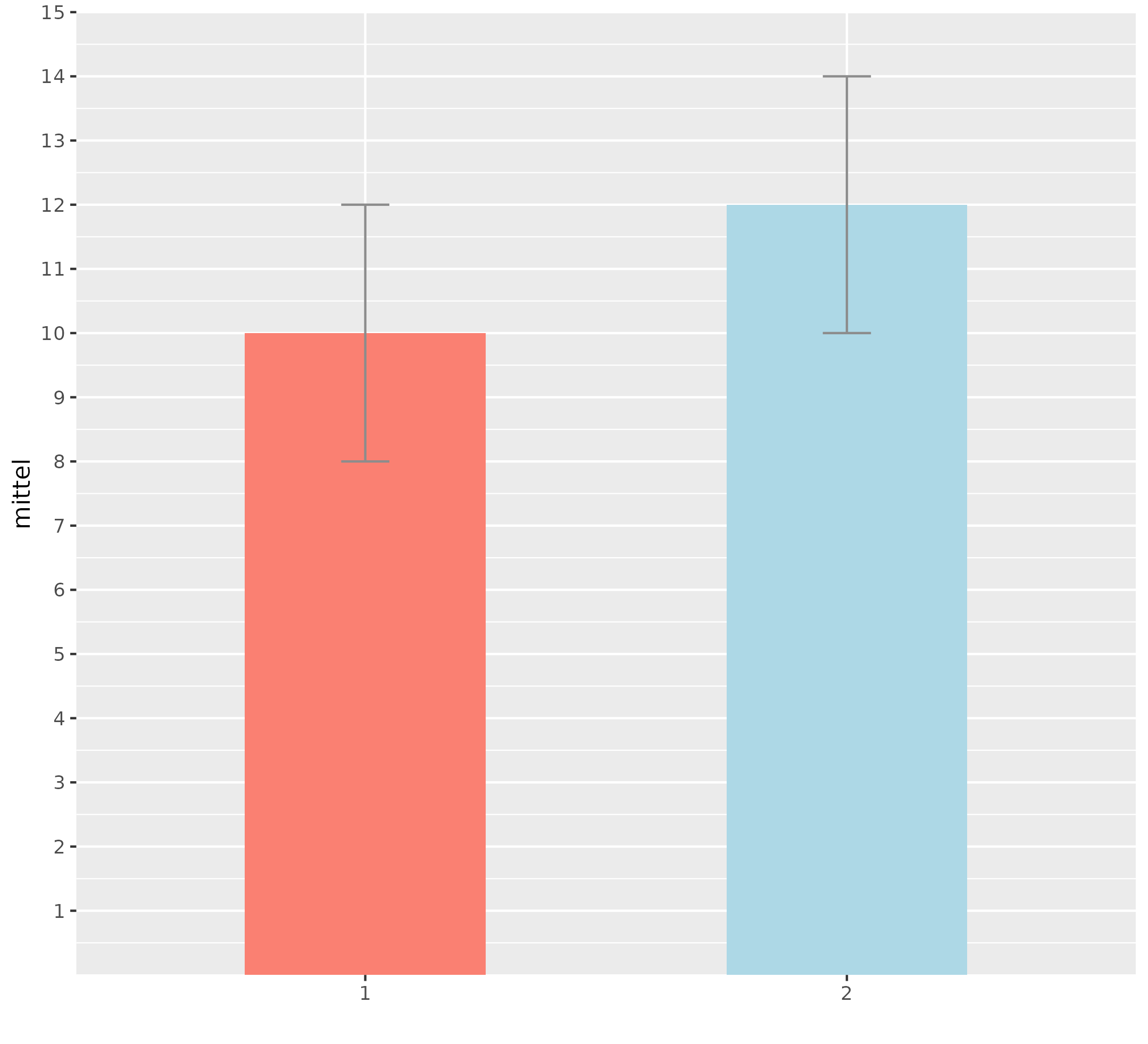
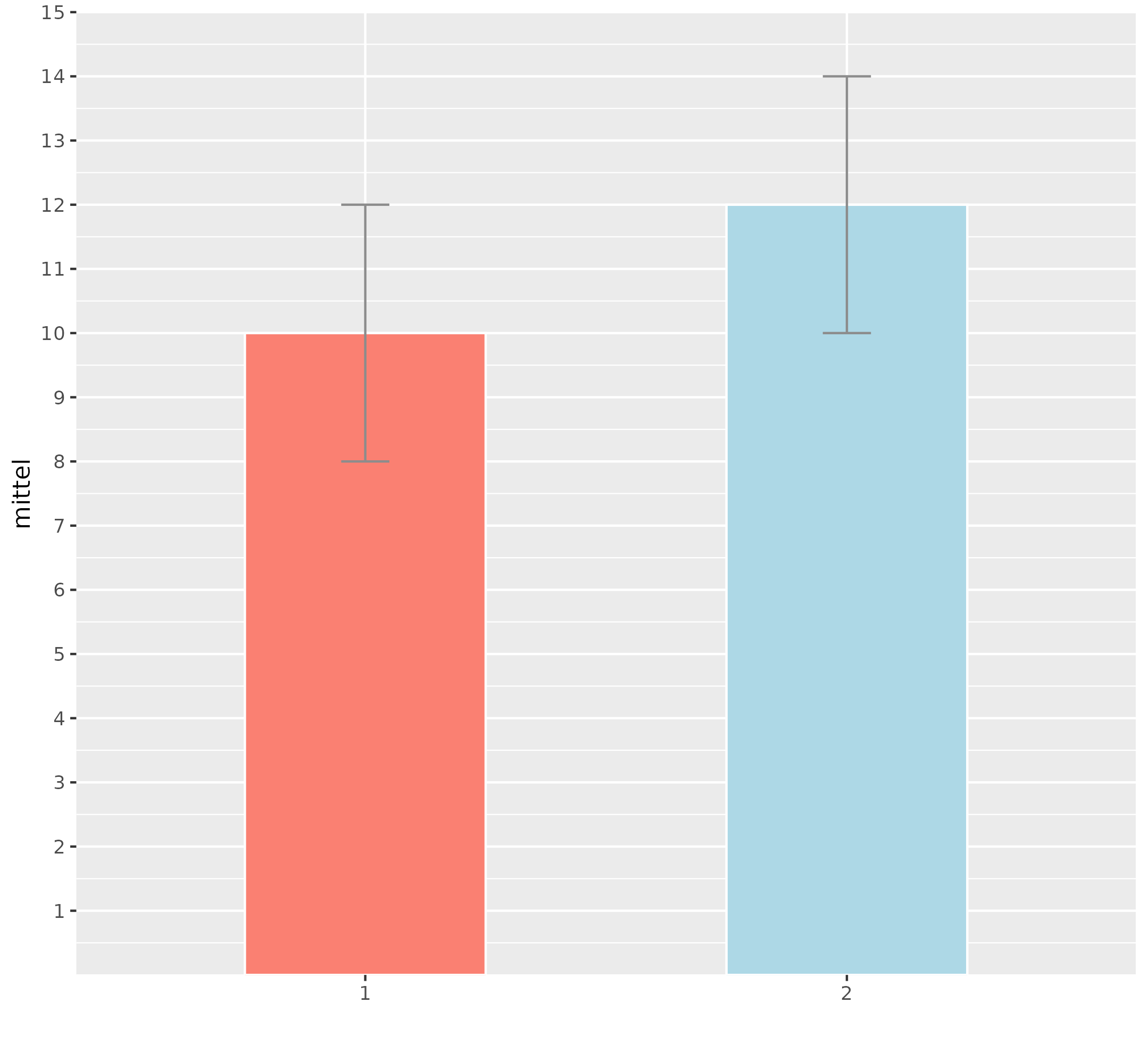
gruppe 1.1701 0.3816 3.066 0.00217 **

Interpretation

Der p-Wert ist hier die wichtigste Statistik. Mit p = 0.00217 kann man die Nullhypothese verwerfen und schlussfolgern, dass die beiden Gruppen mit Blick auf eine Zielhäufigkeit unterschiedlich ansprechen.

Fazit

Ein Regression für Häufigkeitsdaten prüft, ob die Gruppenzugehörigkeit eine Vorhersage erlaubt bzw. ob Gruppen unterschiedlich in Ihrer Häufigkeit sind. Im Beispiel sah man höhere Besserungshäufigkeiten in der zweiten Gruppe, während die andere Gruppe weit darunter lag. Interpretativ könnte man folgern: Die zweite Gruppe hat höhere Besserungsraten, sie profitiert mehr.