Eine Partialkorrelation klärt die Frage, ob zwei Variablen immer noch korrelieren, wenn man eine dritte Variable "abzieht" (herauspartialisiert). Beispiel: An den Daten eines Sommers ergibt sich eine Korrelation zwischen der Menge an verkaufter Eiskreme und der Häufigkeit von Sonnenbränden. Verursacht Eiskreme, dann einen Sonnenbrand? Natürlich nicht, der dritte Faktor ist die Anzahl an täglichen Sonnenstunden, diese ist höher, wenn auch viel Eiskreme verkauft wird und mit jeder weiteren Sonnenstunden steigt die Anzahl an Sonnenbränden. Ich würde empfehlen, die Rangvarianzanalyse mit dem R zu rechnen. Kopieren Sie die nachfolgenden 3 Zeilen in Ihr R-Studio.

Wir erstellen zuerst Zufallsdaten (x, y, z, wobei x = Eiskrememenge, y = Sonnenbrände, z = Drittvariable Sonnenstunden), dann rechnen wir den Einfluß von z (Sonnenstunden) weg.

set.seed(123)
x <- rnorm(50)
y <- 2 * x + rnorm(50)
cor(x, y)

Wie erkennbar, hängt in diesem Beispiel y von x einfach um den Faktor 2 ab (mit normalverteilten Zufallszahlen drum herum). Diese Abhängigkeit zeigt sich auch in der Korrelation, diese ist r = 0.895.

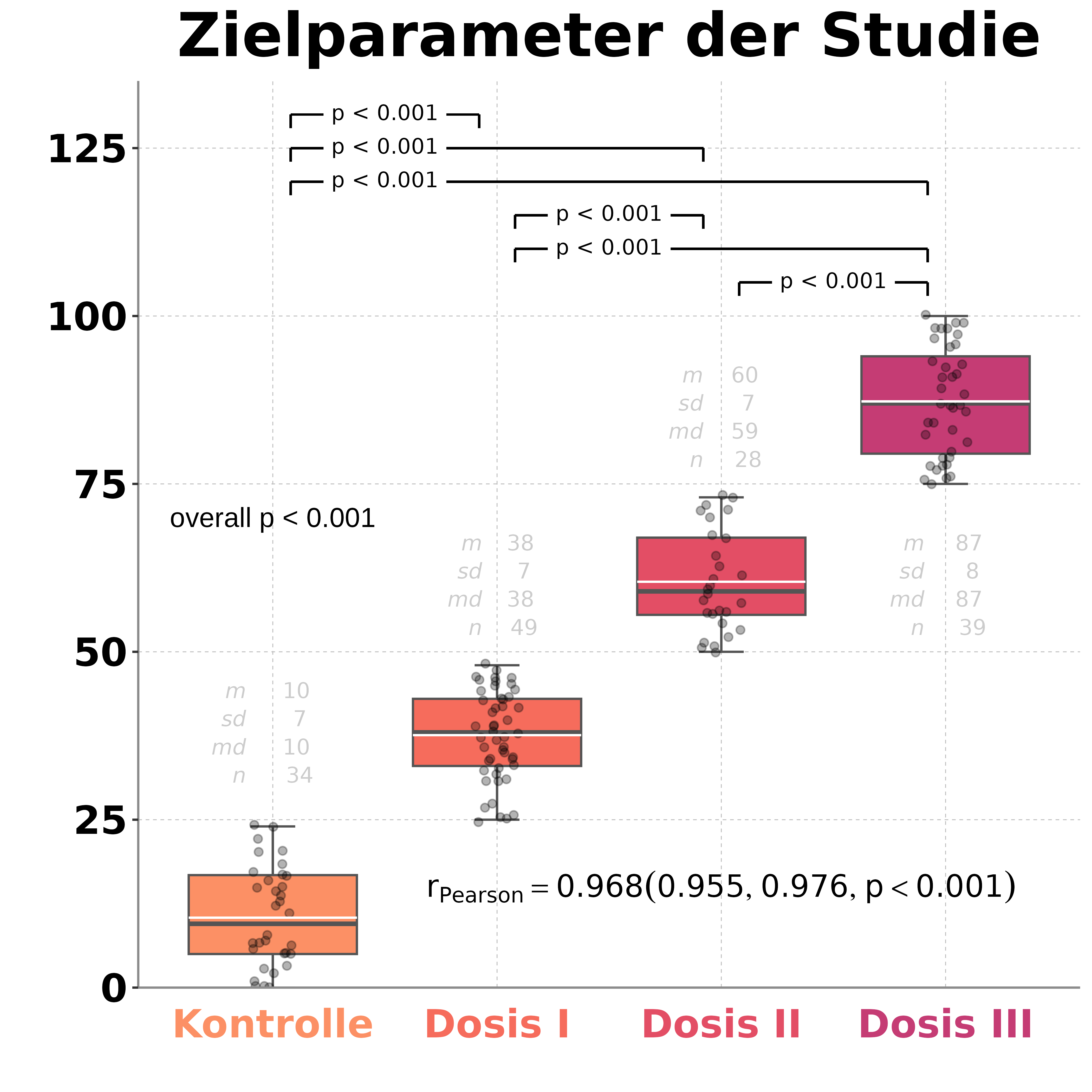
z <- 0.5 * x + 2 * y + rnorm(50)

Wie erkennbar, hängt in diesem Beispiel z sowohl von x als auch von y ab (mit normalverteilten Zufallszahlen drum herum).

Baut man das ganze nun in einen data.frame, partialisiert die Werte heraus, d.h. man verwendet ab jetzt die z-freien Werte von x und z-freien Werte von y (die jeweils vorhergesagten Residuen werden abgezogen), dann erhält man eine wesentlich geringere und deutlich näher bei Null liegende Korrelation von r = 0.132.

daten <- data.frame(x, y, z)
y_aus_z = lm(y ~ z, data = daten); y_bereinigt_um_z <- residuals(y_aus_z)
x_aus_z = lm(x ~ z, data = daten); x_bereinigt_um_z <- residuals(x_aus_z)
# Partielle Korrelation zwischen resid_x und resid_y
cor(x_bereinigt_um_z, y_bereinigt_um_z)

Die Höhe der Korrelation ist hier die wichtigste Statistik. Mit r = 0.132 korrelierten unser simulierter Eiskremeverkauf (x) und das Auftreten an Sonnenbränden (y). Zieht man die Sonnenstunden (z) ab, dann ergibt sich im Beispiel keine Korrelation mehr (sie ist wesentlich näher an Null).

Fazit

Eine Scheinkorrelation kann mit Hilfe einer Drittvariablen bereinigt werden, der r-Wert bewegt sich dann in die Nähe einer Nullkorrelation. Der Verbrauch von Eiskreme, dessen Höhe erst mit der Anzahl an Sonnenbränden scheinbar korrelierte (r = 0.895), fällt in sich zusammen (r = 0.132), wenn man die Anzahl der Sonnenstunden berücksichtigt. Diese bestimmte sowohl den Eiskremeverkauf, als auch das Auftreten von Sonnenbränden. Zieht man den Einfluß von letzterem ab, fällt die Schein-Korrelation wie ein Kartenhaus in sich zusammen.