Ein Mediantest klärt die Frage, ob 2 Gruppen voneinander abweichen, nachdem man sie am Gesamtmedian gesplittet hat.
Die Idee ist, dass eine der beiden Gruppen häufiger unterhalb des Medians liegt als die andere. Die Nullhypothese lautet, dass es keinen Zusammenhang von Median und Gruppe gibt.
Ein Beispiel ist, ob ein Besserungswert bei schwerer Erkrankten geringer ausfällt, oder (allgemeiner formuliert), ob ein Change in 2 Subgruppen meiner Stichprobe unterschiedlich verläuft.
Ich würde empfehlen, den Mediantest mit dem R zu rechnen. Kopieren Sie die nachfolgenden Zeilen in Ihr R-Studio.

mydata = data.frame(gruppe = (1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2), change = c(3,5,4,4,4,4,4,4,5,5,2,4,2,2,1,2,3,2,2,3) median_test(change ~ factor(gruppe), data = mydata)

Das ergib den folgenden Ausdruck:

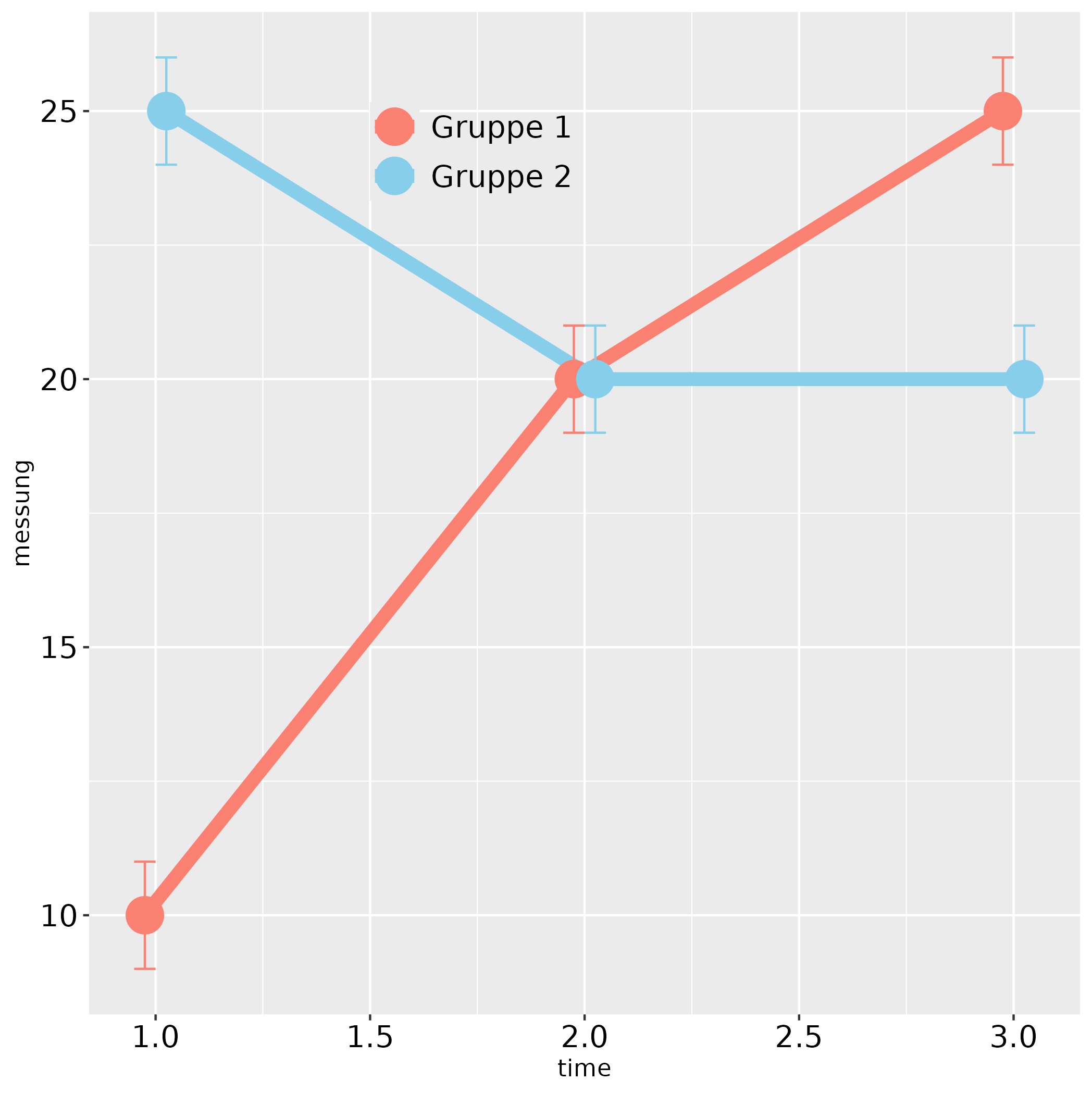
Asymptotic Two-Sample Brown-Mood Median Test
data: change by factor(gruppe) (1, 2)
Z = 3.4871, p-value = 0.0004883

Der p-Wert ist hier die wichtigste Statistik. Mit p = 0.0004883 kann man die Nullhypothese verwerfen und schlussfolgern, dass der Change in den beiden Gruppen unterschiedlich verläuft.

Fazit

Ein Mediantest prüft, ob meine Zielvariable anders ausfällt, wenn man den Gruppenmedian in die Betrachtung einführt. Im Beispiel sah man eine stärkere Besserung in der zweiten Gruppe, deren Besserung liegt häufiger oberhalb der Mitte (Median), während die andere Gruppe weit darunter lag. Interpretativ könnte man folgern: Die zweite Gruppe ändert sich stärker, sie profitiert mehr.